Grashof’s Law | The Triple Rocker Mechanism | Double Crank Mechanism | Double Rocker Mechanism | Crank and Rocker Mechanism

Grashof’s Law

Grasoff’s law states that for a four-time linkage system, if the sum of the shortest and longest lengths of a planar quadrilateral linkage is less than or equal to the sum of the remainings two links, then the shortest link is independent of respect.

It can be rotated to a neighboring link. In a four-bar series, there are four turning pairs and no sliding pairs.

Mark the shortest link of the four-bar linkage with S and the longest link by L, and the other two links by P & Q.

The necessary condition to satisfy the Grashoff law is:

S + L ≤ P + Q

This situation is divided into two cases: –

• Now, Let Us See the First Case, I.e., S + L < P + Q.
• Now, Let Us See the First Case, II.e., S + L = P + Q.

Also, Read: What Is Pirani Gauge? | Working of Pirani Gauge | Construction of Pirani Gauge | Principle of Pirani Gauge

Case I.  S + L < P + Q:

By fixing different links one at a time, this case produces three mechanisms. These mechanisms are:-

• Double Crank Mechanism.
• Double Rocker Mechanism.
• Crank and Rocker Mechanism.

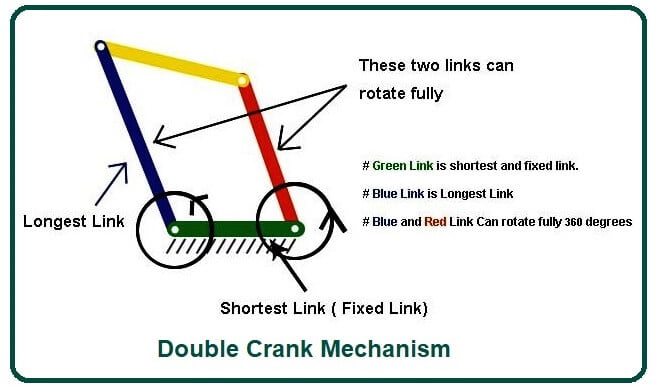
#1. Double Crank Mechanism-

• It is also known as the crank mechanism or drag link mechanism.
• In the double crank mechanism, the shortest link that is s is fixed or grounded. In this mechanism, both links on a fixed link can rotate 360 degrees.

Also, Read: Domestic Electrolux Refrigerator | Different Components of Domestic Electrolux Refrigerator

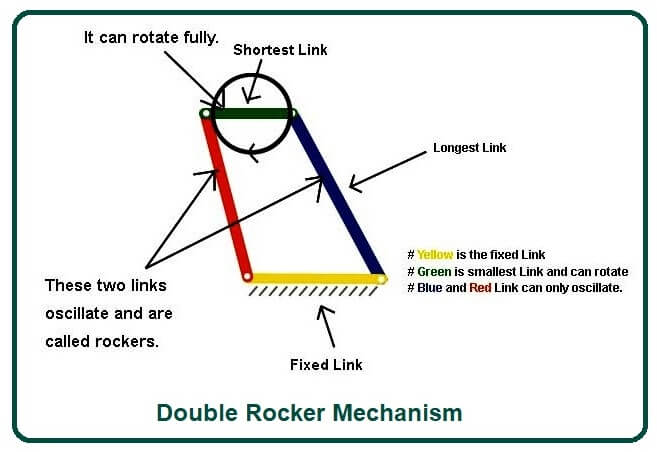
#2. Double Rocker Mechanism-

• In a double rocker mechanism, the link is fixed or grounded as opposed to the shortest link.
• In this system, the shortest link can rotate 360 degrees.
• The shortest link is called a coupler. Both links given to a fixed link can oscillate. These two links are called rockers.

Also, Read: Inversion of Double Slider Crank Mechanism

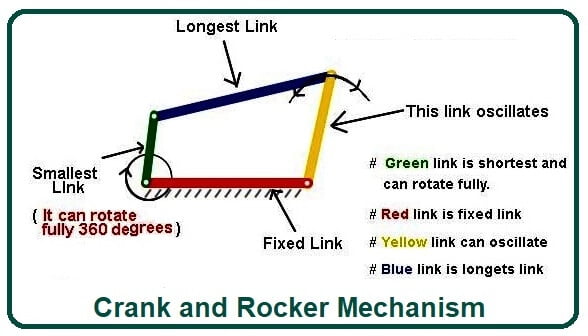
#3. Crank and Rocker Mechanism-

• In the crank and rocker mechanisms, the link adjacent to the shortest link is fixed or grounded.
• In this system, the shortest link rotates, and the second link is caught by fixed link oscillations.

Also, Read: Working of Kaplan Turbine | What Is a Kaplan Turbine? | Main Parts of Kaplan Turbine

Case II. S + L = P + Q:-

In such a kinematic chain, the links become collinear at least once per revolution of input cranks.
This case is divided into two cases: –

• Case 1:- Length of All Links Are Distinct.
• Case 2:- Length of Any Two Link Are Same.

Case 2.1:- Length of All Links Are Distinct-

If the length of any two links is the same, then the length of the remaining two links will also be the same because of the equation S + L <P + Q.

Case 2.2:- Length of Any Two Link Are Same-

If the length of any two links is the same, then the length of the remaining two links will also be the same due to the equation S + L < P + Q.

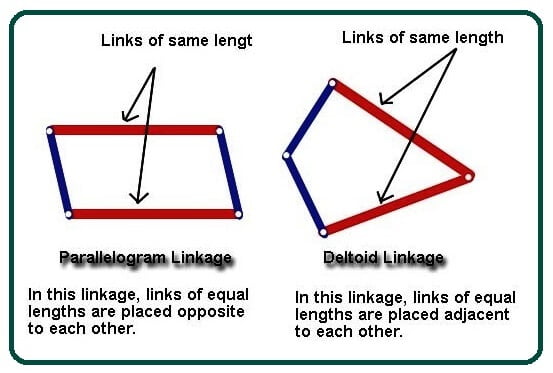
In such a case, two links are possible depending on the placement of the link: –

• Parallelogram Linkage:- In this linkage, links of equal length are placed opposite to each other.
• Deltoid linkage:- In this linkage, links of equal length are placed adjacent to each other.

In both cases, the inversions obtained are either a crank winding or a double crank mechanism.

These two linkages change the situation when the links collide.

In the change point state, the output crank speed becomes unpredictable. It can go either of two ways. The inversion is a crank winding or double crank, depending on the speed of the output crank in the change point position.

Now let’s looks at the case when the length of the shortest and longest link is greater than the length of the remaining two links.

Ie S + L> P + Q

In this case, no single link can make a complete revolution, regardless of whether the four-link is fixed. So, in this case, there is only one inverse, and that is.

Also, Read: Vane Blower Compressor | Construction of Vane Compressor | Working of Vane Compressor

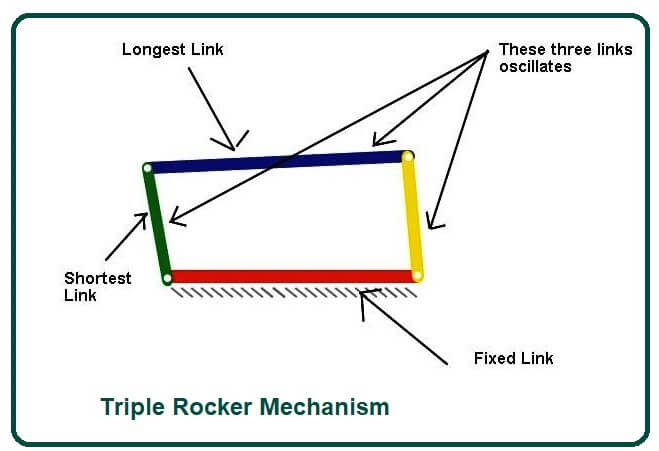
The Triple Rocker Mechanism

• In this mechanism, no link will be able to make a full revolution.
• All three links will oscillate except for the fixed links. These three links are called a rocker, and hence this mechanism is called the triple rocker mechanism.

Also, Read: Keyless Remote Battery Is Low | When Does Key Fob Battery Replacing Replacing? | How to Replace a Keyless Remote Battery

---

Frequently Asked Questions (FAQ)

Grashof’s Law

Grashof’s Law states that for a planar four-bar linkage system, the sum of the shortest and longest link lengths cannot be greater than the sum of the remaining two link lengths if there is to be a continuous relative rotation between two members.

Triple Rocker Mechanism

In the Triple rocker mechanism, one link is fixed while the other three oscillate. It is a nongraphic linkage for which the sum of the lengths of the shortest link and the longest link is greater than the sum of the lengths of the other two links.

Double Crank Mechanism

The double Crank Mechanism converts a reciprocating motion to a rotational motion and vice versa. The interest in this mechanism is that it has three moments of standstill. This project aims at carrying structural analysis of the mechanism with two different loading configurations.

Double Slider Crank Mechanism

The double slider crankshaft has two sliding pairs and two twist pairs. It is named the double slider crankshaft because it has two sliding pairs. It has two sliders, a frame in which the slider moves, and a link that connects the two slides and fixes the distance between the two sliders.

Double Slider Crank Chain

The double slider crankshaft has two sliding pairs and two twist pairs. It is named the double slider crankshaft because it has two sliding pairs. The frame in which sliders move is a combination of two straight grooves that form a single link and cut eaches other at right angles.

Crank Rocker Mechanism

The crank–rocker mechanism is, basically, a four-bar mechanism in which the output link oscillates when the input link completely rotates, consistent with Grashof’s Law.

Crank Rocker Mechanism Application

The crank rocker mechanism is a common mechanism widely used in a sewing machine, mixer, shaper, and other equipment.

---